The purpose of this example is to mesh a 2d rectangle by triangles and to partitionize the nodes whose coordinates verify f(x,y,z)<=0 from the other nodes.
The graph is composed by
- nodes with coordinates & state in {0,1}
- ports with no state.
Nodes are the summit of the triangles & the ports are placed on its edges.
We want to select all the node whose coordinates verify f(x,y,z)=x-y<=0.
For each triangle whose one summit' state is different from the 2 each others, a new triangle is added with its summits are in the middle of the edges of the pattern triangle.
The f(x,y,z) is computed for each new nodes & the state is sate to 1 if the functon is positive and 0 otherwise.
The initial, pattern & transform graphs are as follow:
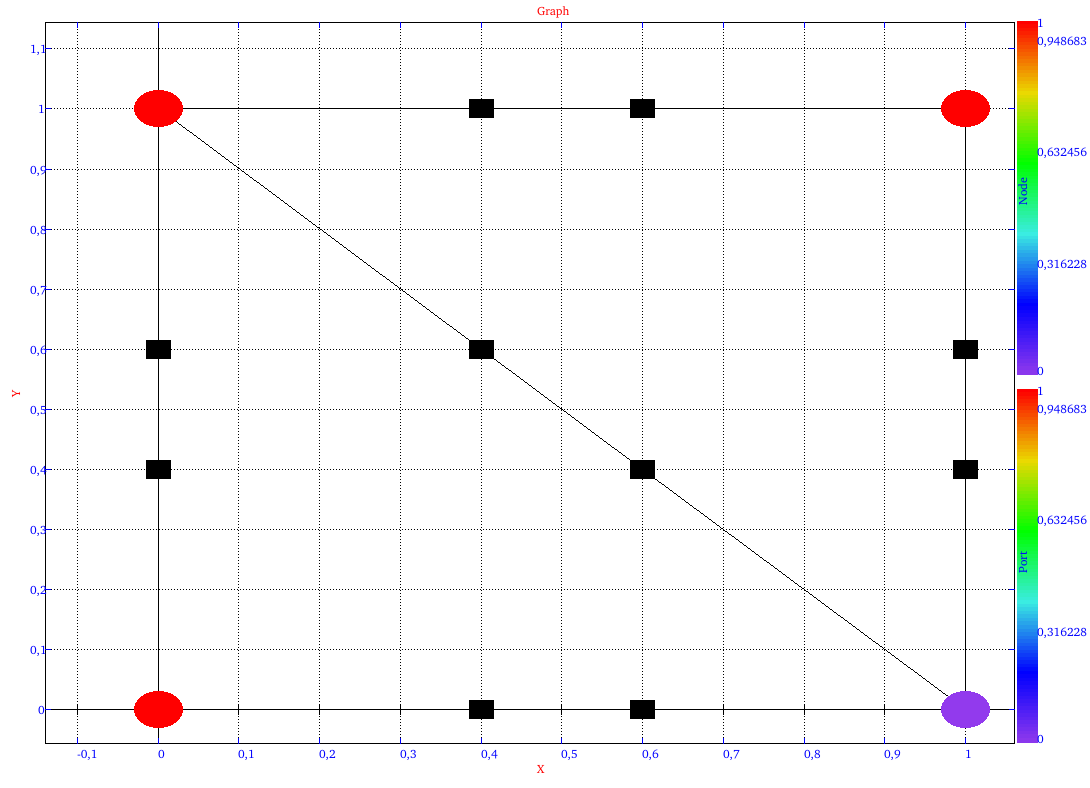 |
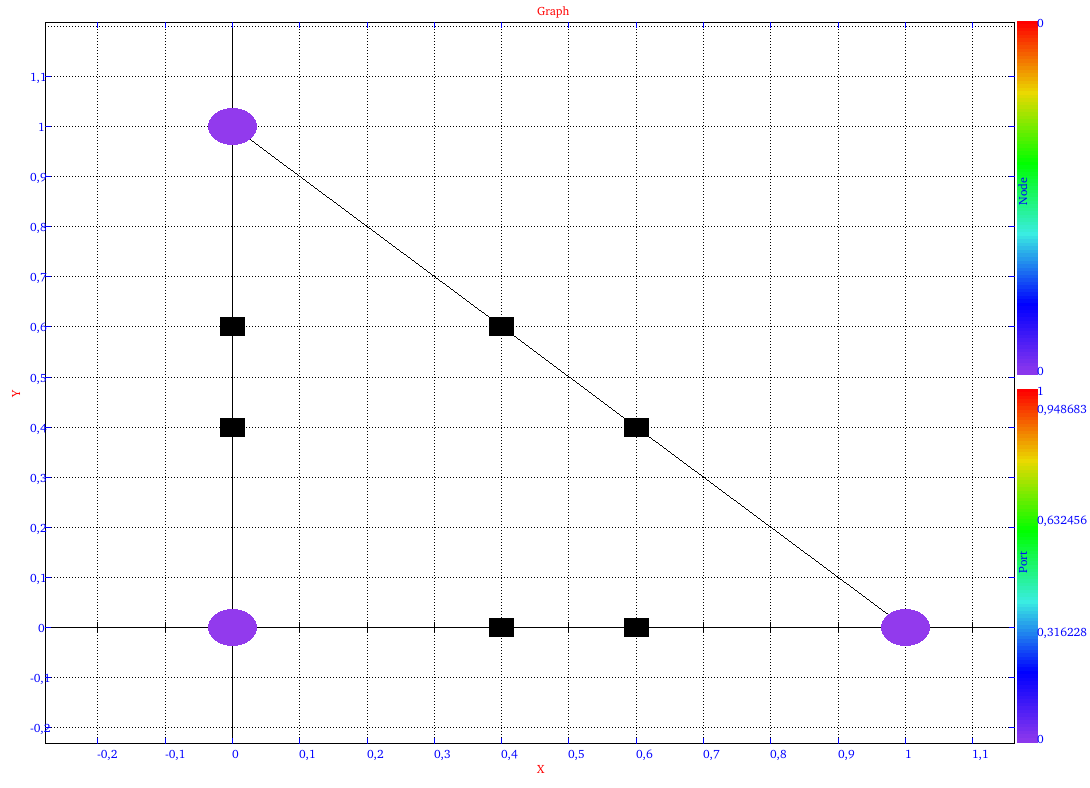 |
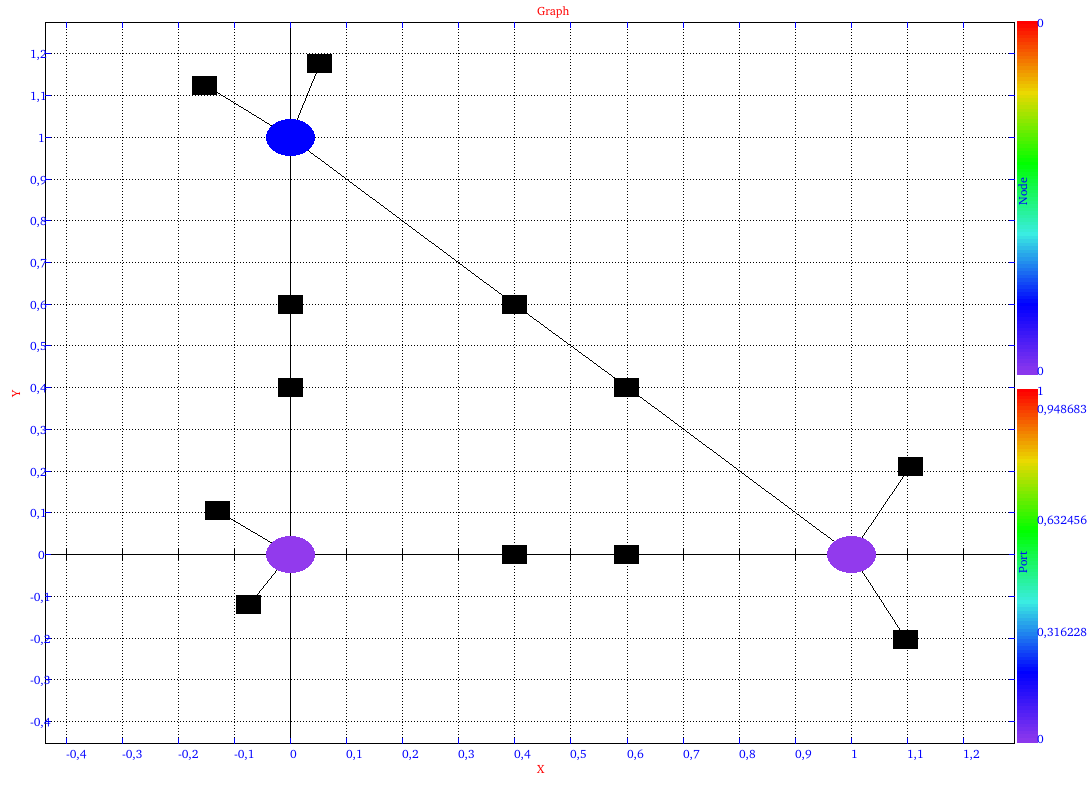 |
| initial graph | pattern graph | transform graph |
The rule of the graph consists in
- removing the edges between 2 ports of the pattern triangle
- adding connections between the freed pattern graph ports and the freed transform graph ports
- update the coodinates & states of the new nodes
- the mapping rules are to
- disable the mapping of triangles by permutation of its summits (isUpToAutomorhism=true)
- valid the mapping by testing if one of state of pattern node is different from the 2 others.
the rule is written as follow:
To compute the 3 first rewriting graph, execute the command:
The results of the rewriting graphs are as follow:
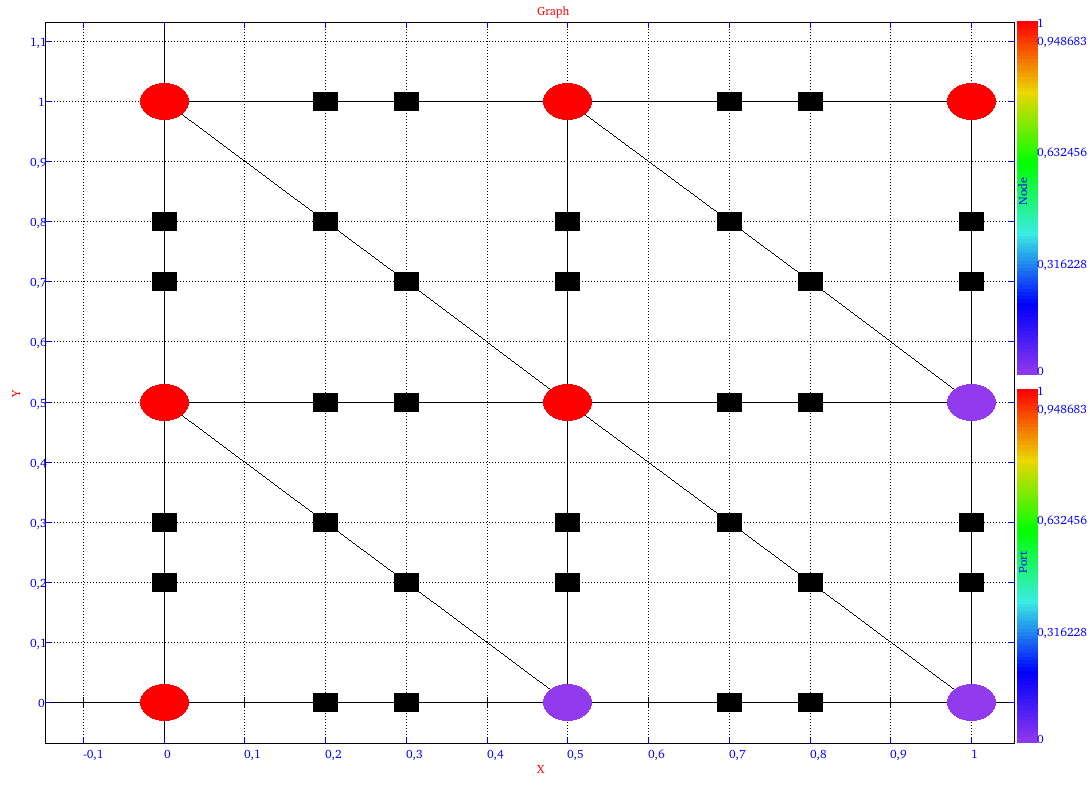 |
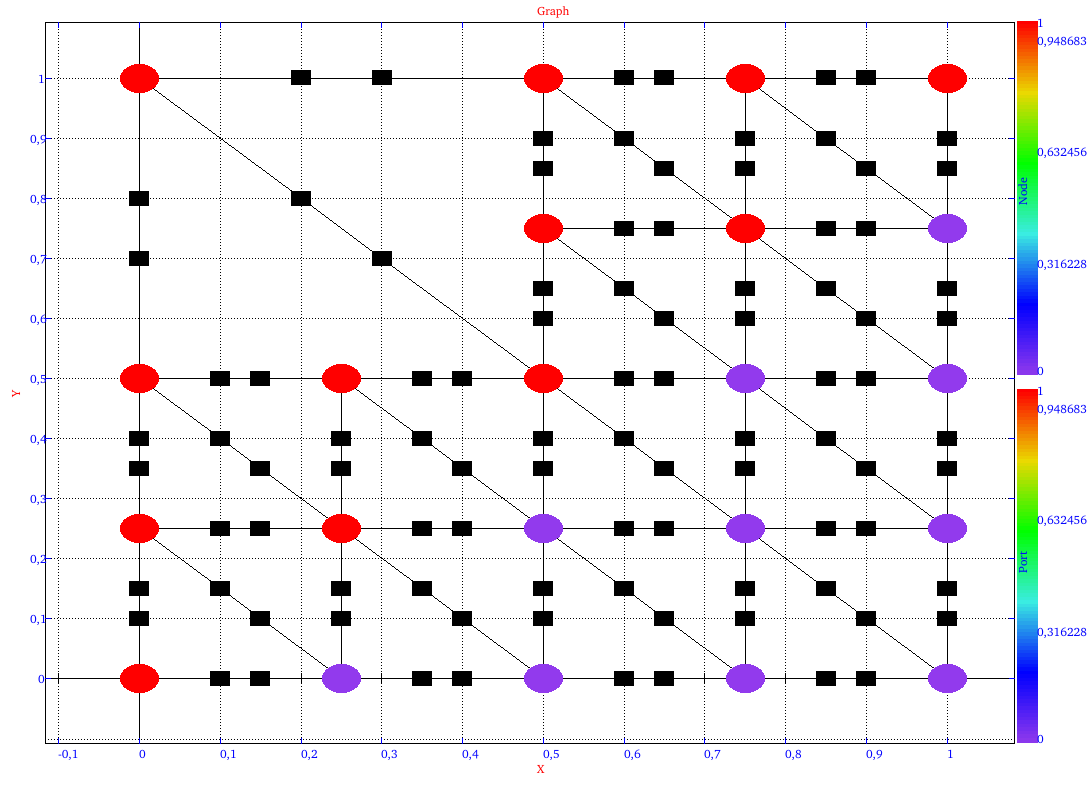 |
| rewriting graph at iteration 1 | rewriting graph at iteration 2 |
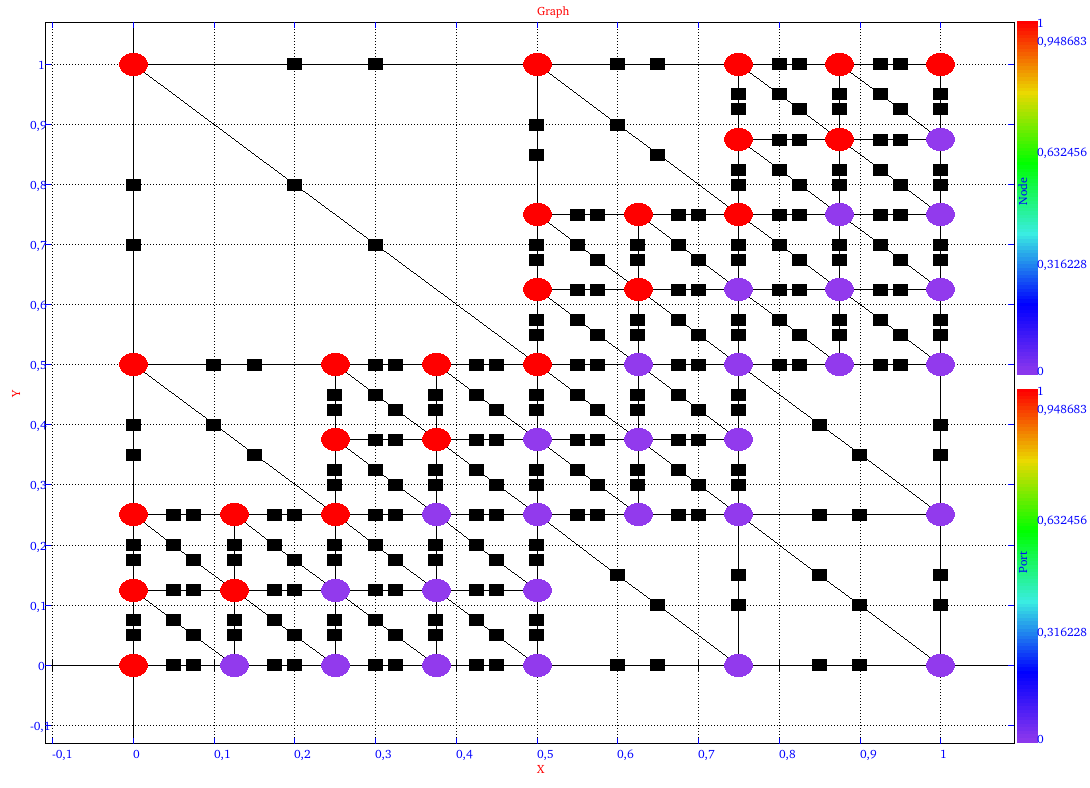 |
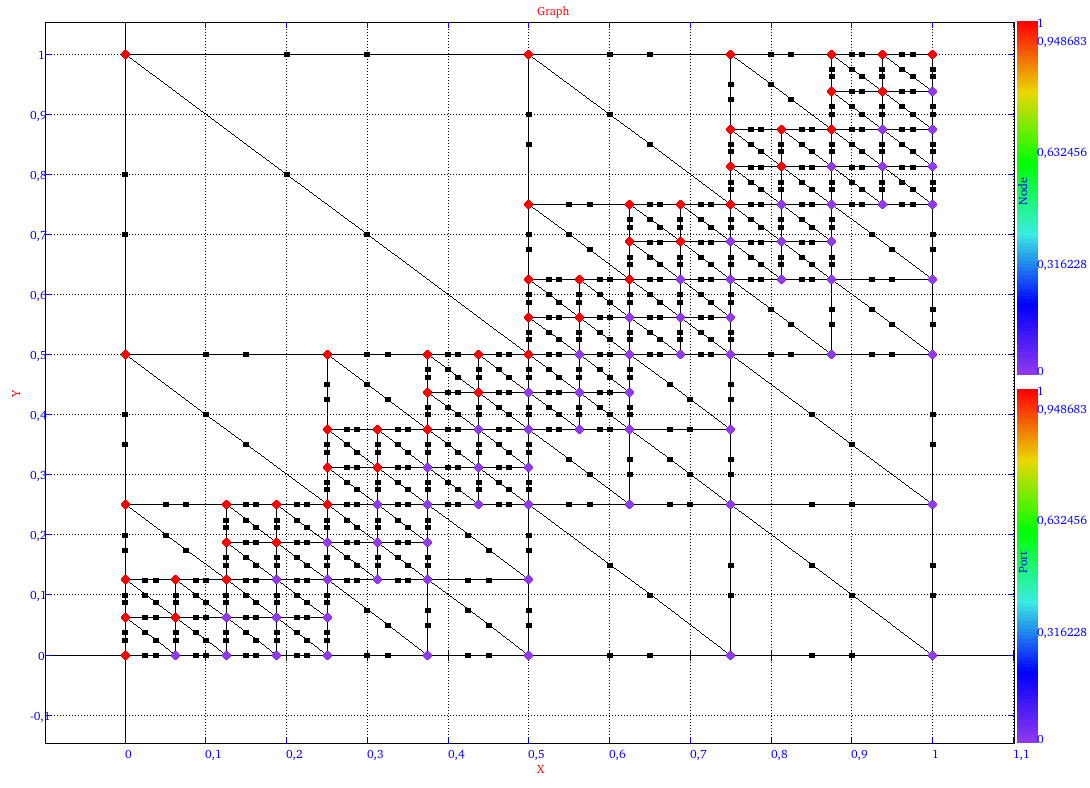 |
| rewriting graph at iteration 3 | rewriting graph at iteration 4 |
 1.8.8
1.8.8